Here, we will display some MCQ questions on Scales in Engineering drawing. Hope, you will get interest in solving those. You may download the MCQ sheet by clicking on the PDF button located in the end of the article.
Now, let’s start the MCQ on Scales.

Quiz on Scale or Viva Questions
You may consider this as a test of 20 marks. After completion of the test, you can check the answers and can come to know how much you are prepared.
Overview
Are you trying to find out the explanations of the answers of the MCQ questions? If yes, then scroll down and find the explanations here only.
Scale in Engineering drawing
A scale is defined as the ratio of the linear dimensions of the object as reflected on the drawing to the actual dimension of the object.
With the help of scale, we can get the actual dimensions of the object though they are not mentioned in the drawing.
Different types of scales
There are different types of scales:
- Plain scale
- Diagonal scale
- Comparative scale
- Vernier scale
Here, we will discuss about plain scale and diagonal scale.
Plain Scale in Engineering Drawing
A plain scale is a scale where two units are displayed. As for example: when you need to measure 5.6 m or 8.2 cm; you need plain scale.
5.6 m means 5 meters and 6 decimetres. So, here two units are involved. Similarly, for 8.2 cm means 8 centimetres and 2 millimetres. So, here also you need plain scale.
It consists of a line which is divided into few parts. The first part is again divided into smaller parts.
At the end of the first part, ‘0’ is mentioned. Below the ‘zero’, two arrows are shown. One arrow indicates left side and another arrow indicates right side.
Diagonal Scale in Engineering Drawing
A diagonal scale is a scale from where students will get three units.
As for example: when you need to measure 5.63 m or 8.25 decimetres; you need diagonal scale.
5.63 m means 5 meters, 6 decimetres, and 3 centimetres. So, here three units are involved. Similarly, for 8.25 decimetres means 8 decimetres, 2 centimetres, and 5 millimetres. So, here also you need diagonal scale.
It also consists of a line which is divided into few parts. The first part is again divided into smaller parts. These smaller parts are connected with each other diagonally which we will show in the drawings.
Differences between Plain Scale and Diagonal Scale
| Plain scale | Diagonal scale |
| We can measure the dimensions. | measure the dimensions more accurately. |
| We can measure two units | measure three units |
| e.g. 2.3 decimetres, 9.5 meters | e.g. 3.45 decimetres, 8.76 meters. |
What is R.F in Engineering Drawing?
The full form of R.F is representative fraction. It is a ratio of any dimension of the object shown in the drawing to that of the actual dimension of the object.
R.F=(Drawing dimension / actual dimension)
Classification of Scales Depending on R.F
Depending on R.F, scales can be divided into three categories:
Full Scales
When drawing dimension is same as that of actual dimension, the scale is called as full scale.
In full scale, R.F=1
If you want to draw your pen in a drawing sheet; you can draw the same size of pen.
Reduced Scales
When drawing dimension is less than that of the actual dimension, the scale is called as reduced scale.
In this case, R.F<1
If you want to draw a building, can you accommodate the building within the drawing sheet? It is not possible.
Therefore, you have to reduce the size of the building while showing it on the drawing. Drawing size will be less than that of the actual size.
Enlarged Scales
When drawing dimension is more than that of the actual dimension, the scale is called as enlarged dimension.
In this case, R.F>1
When you want to draw internal layout of the instruments of your wrist watch, if you draw the same size; the instruments will not be visible.
Therefore, you have to enlarge the dimensions proportionately on the drawing. Here, drawing dimension is more than that of the actual dimension.
Expression of Scales
Scales can be expressed in the following three ways:
Engineer’s Scales
In this case, the relation between the dimension of the object on the drawing and the actual dimension is mentioned in this way: 20 mm= 2 m.
Graphical Scales
The scale is drawn on the drawing itself. This has one disadvantages. When the drawing becomes old, the scale may not be visible which may provide wrong information.
Representative Fraction
In this case, below the drawing it is written as R.F= 0.001
How to Draw the Scales
We will explain this by giving one example:
Example Problem
Construct a scale of 1:4 to show centimetre and long enough to measure upto 5 decimetres. Mark 3.8 dcm.
- Given: R.F = ¼
- Actual length= 5 dcm = 50 cm
- Length on Drawing= 50×1/4=12.5 cm
Process How to Draw a Plain Scale
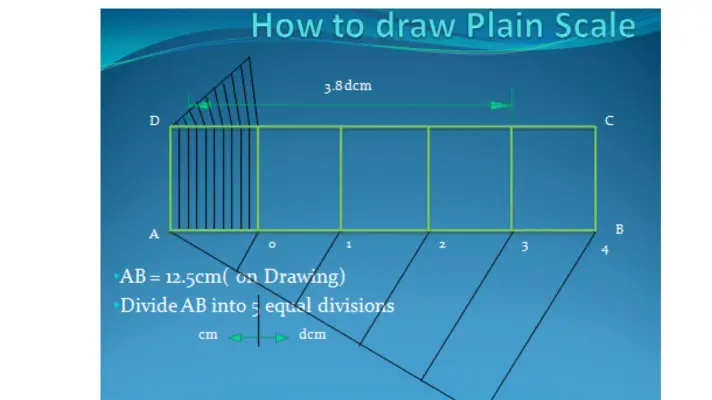
Draw a line AB of 12.5 cm length. Draw perpendicular lines AD from point A and BC from point B. AD=BC
You can take any width of the scale. Here, we have taken AD as 3cm. You may take 2cm or 2.5 cm also.
Divide AB into 5 equal divisions.
Why to divide into 5 equal divisions? It is because the actual length of the scale is 5 decimetre. So, if we divide AB into 5 equal divisions, each division will give you 1 decimetre.
At the end of first division, mark as ‘0’. Mark the next division as ‘1’. In this way, you mark the division lines as ‘2’,’3’, and ‘4’.
A0=01=12=23=34= 1 decimetre= 10 centimetre
Now you divide A0 i.e. the first division into 10 equal divisions. Each division will give you 1 centimetre.
So, 0 to B will indicate decimetre scale and 0 to A will indicate centimetre scale.
Now, you have to mark 3.8 decimetre on this scale. So, you take 3 decimetres from the right side scale i.e. 0 to B scale. Balance 8 centimetres, you take from the left side scale i.e. 0 to A.
How to Draw the Diagonal Scales
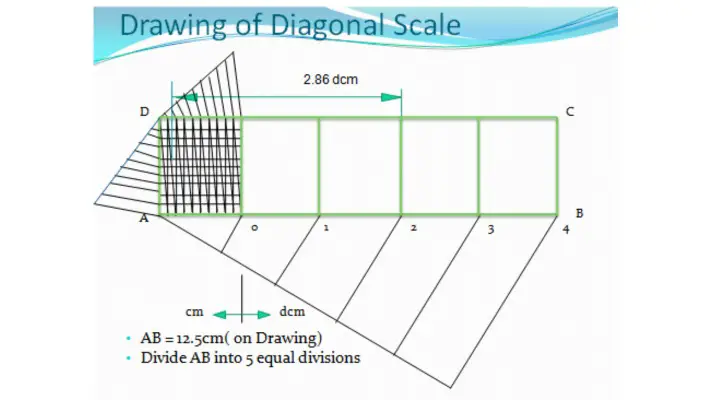
For the above mentioned problem, if you have to mark 3.82 decimetre; then you have to draw the diagonal scale.
For drawing the diagonal scale, first you have to draw the plain scale in the above mentioned way.
In the left side scale, each small division = 1 centimetre = 10 milimetres
This small division will also be divided into ten equal divisions. This each new division will give you 1 milimetre as shown in the drawing.
The multiple-choice questions mentioned here are the basic questions from the chapter-“The construction of Scales”. I hope that it will help you in clearing the viva during semester examination. Thank you. Best wishes.


