Engineering Curves –MCQ Questions and Answers [PDF Included]

Hello Students!  In this article, I will display some Multiple-Choice Questions on Engineering Curves. When you have to draw the polygon, Ellipse, Parabola, etc. in your Engineering Drawing Lab, you may refer to this sheet.  You will get the entire process to draw the curves. Also, you will find Engineering Curves MCQ Questions and Answers.

If you want to take the PDF format of this article, you may click the downloadable button located at the end of this article.

MCQ Questions on Engineering Curves

• In an Ellipse, parabola, the fixed point is known as:

1. Focus
2. Directrix
3. Axis
4. None of these

Ans: (1)

• In an Ellipse, parabola, the fixed-line is known as:

1. Focus
2. Directrix
3. Axis
4. None of these

Ans: (2)

• The eccentricity is the ratio of:

1. Distance of the point from the focus and distance of the point from the directrix.
2. Distance of the point from the directrix and distance of the point from the focus.
3. Distance of the point from the vertex and distance of the point from the directrix.
4. Distance of the point from the focus and distance of the point from the vertex.

Ans: (1)

• The eccentricity of an Ellipse is:

1. Greater than 1
2. Equal to 1
3. Less than 1
4. 0

Ans: (3)

• The eccentricity of a Parabola is:

1. Greater than 1
2. Equal to 1
3. Less than 1
4. 0

Ans: (2)

• The eccentricity of a Hyperbola is:

1. Greater than 1
2. Equal to 1
3. Less than 1
4. 0

Ans: (1)

• If the section plane is inclined to the axis of the curve and cuts all the generators on one side of the apex, the section is a/an:

1. Ellipse
2. Parabola
3. Hyperbola
4. Circle

Ans: (1)

• If the section plane is inclined to the axis of the curve and is parallel to one of the generators, the section is a/an:

1. Ellipse
2. Parabola
3. Hyperbola
4. Circle

Ans: (2)

• If the locus of a point that moves in a plane and the ratio of its distances from a fixed point and the directrix is always constant, then the locus is of a/an

1. Ellipse
2. Parabola
3. Hyperbola
4. Conic

Ans: (4)

• Which of the following curves are used in the tooth profile of gears of a dial gauge?

1. Ellipse
2. Parabola
3. Hyperbola
4. Cycloidal curves

Ans: (4)

How to Construct the Engineering Curves

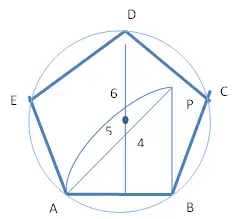
• Construct a Polygon of sides 5 cm each.

Steps:

1. Draw a line AB of 5cm.
2. At point B, draw a line BP that is perpendicular to AB and BP=AB
3. Join the points A and P and get AP.
4. Consider centre point as B, take radius as AB, draw the arc AP.
5. Bisect AB at point 4. So, A4 = B4. Name the intersecting point of arc AP and bisecting line as 6. Name the mid-point of 4-6 as 5.
6. Take the centre point as 4 and radius as A4. You will get a circle within which you can insert a Square.
7. Measure the distance from 4 to 5. Take the same distance with the help of divider and mark the points as 6,7,8,etc.
8. If you want to draw a pentagon, draw a circle considering the centre point as 5 and radius as A5. Take the arc as AB, put the campus at point A. Then, cut the arcs on the circle. Name the point as E. Put the campus at point B. Cut the arc on the circle. Name the point as C. Now , put the campus at E and C and then cut the arcs on the circle. You will see that both the arcs intersect each other at point D. In this way, you will get the Pentagon ABCDE.
9. If you want to draw a hexagon, draw a circle considering the centre point as 6 and radius as A6. Draw the hexagon within this circle.

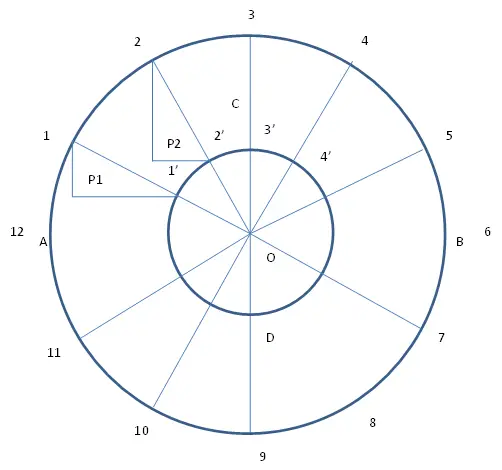
• Construct an Ellipse by Concentric Circle Method.

Draw an Ellipse. Major Axis = 100 mm and Minor Axis = 60 mm

Steps:

1. Draw a line AB of 100 mm
2. Get the mid point of AB. Name it as “O”.
3. Draw a perpendicular line at O. Name it as “CD”
4. CD = 60 mm and OC=OD
5. AB is Major axis and CD is Minor Axis
6. Take center as “O” and diameter as AB, draw a circle.
7. Take center as “O” and diameter as CD, draw another circle.
8. Divide the major circle into 12 numbers of equal divisions. Name the division points as 1,2,3,…,10,11,12.
9. These O1,O2,O3,O4…..,O11,O12 lines are cutting the minor circle say at points 1’,2’,3’,4’,..10’,11’,12’.
10. Draw a vertical line from point 1 so that it becomes parallel to the line OC. Also, draw a horizontal line from point 1’ so that it becomes parallel to OA. Now, these horizontal and vertical lines will intersect at point P1.
11. Similarly draw the horizontal and vertical lines from the points 2’,3’,4’,….,11’,12’ and 1,2,3,…,11,12.  Name the intersecting points as P2, P3, P4,….,P11, P12.
12. Join the points P1, P2, P3,….P11,P12 with the help of French Curve /Flexible Curve.
13. The shape you got by joining these points is the required Ellipse.

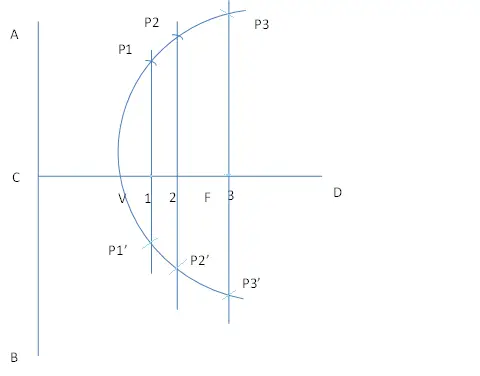
• Construct a Parabola, assuming the distance of the focus from the directrix is 50 mm.

Steps:

1. Draw a vertical line AB. Take a point on AB. Mark it as C.
2. Draw a horizontal line CD.
3. Take a point F on CD such a way, so that FC = 50
4. Bisect CF. Name the mid-point as V as eccentricity of a parabola =1 =VF/VC.
5. Mark a number of points 1, 2, 3, etc. on the line CD. Draw the perpendicular lines through these points.
6. Considering centre as F and arc as C1, draw arcs that will cut the perpendicular line passed through point 1 at P1 and P1’. Similarly, considering centre as F and arc as C2, draw arcs that will cut the perpendicular line passed through point 2 at P2 and P2’.
7. In this way, get the points P3,P3’,P4,P4’,P5,P5’ on both the sides of the axis CD.
8. Join those points with the help of French curve or Flexible curve. Thus get the Parabola.

Conclusion

I hope that you have got the help from this article in drawing the Engineering Curves. Also, I am sure that the Engineering Curves- MCQ Questions and Answers will help you in performing well in your viva. Best Wishes!